Schwingung

Stehende Wellen können sich nicht nur auf schwingenden Saiten, wie im Abschnitt 3.1.1 beschrieben, sondern auch auf angeschlagenen Platten ausbilden. Der deutsche Physiker CHLADNI (1756 - 1827) machte Versuche mit dünnen Platten, auf denen er mit Hilfe von feinem Sand die sog. Knotenlinien ohne Auslenkung und Zonen stärkerer Auslenkung, die jeweils gegenphasig schwingen, sichtbar machte. In Abb. 9 ist eine einfache Schwingungsform einer an den Rändern eingespannten Membran zu sehen, die sich vergleichbar einer Chladiniplatte verhält. Untersucht man die möglichen Frequenzen der Oberschwingungen dieser quadratischen Membran, so stellt sich heraus, dass sie mit der Grundfrequenz im allgemeinen nicht in einem musikalisch harmonischen Verhältnis stehen.

Auch eine Glocke als elastischer Körper kann beim Anschlag freie Biegeschwingungen ausführen, zum einen in Ringform (Umfangsbiegeschwingungen) und zum anderen in Gabelform (Längsbiegeschwingungen). Die Knotenlinien der Umfangsbiegeschwingungen nennt man Knotenmeridiane (m). Sie verlaufen vom unteren Glockenrand senkrecht nach oben über den Scheitelpunkt hinweg und auf der anderen Seite wieder nach unten. Vor allem in etwas älterer Literatur findet man auch die Festlegung, dass die Meridiane oben am Scheitelpunkt enden. Dadurch gelangt man eben beim Zählen zur doppelten Anzahl. Die Knotenlinien der Längsbiegeschwingungen bilden die Knotenkreise (r). (Abb. 10)

Durch die Kombination von m Knotenmeridianen (m = 2, 3, 4...) und r Knotenkreisen (r = 0, 1, 2...) ergibt sich eine große Menge von möglichen Schwingungsformen, von denen jede eine bestimmte Eigenfrequenz besitzt und so genau einen Glockenteilton hervorruft. Der Unterschied zu der quadratischen Membran ist, dass durch die besondere Form der Glocke viele dieser Teiltöne, wie bereits erwähnt, annähernd in musikalisch harmonischen Verhältnissen zueinander stehen. Die Abweichungen sind bei einer guten Glocke so gering, dass sie für das Ohr nicht störend wirken.

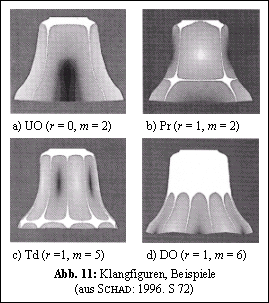
Es wurden schon viele Untersuchungen über die Schwingungsformen angestellt, so dass man die Schwingungsamplituden der Glockenwand heute für jede beliebige Schwingungsform graphisch als Klangfigur sichtbar machen kann.

Seit den achtziger Jahren wird dabei eine moderne Computermethode angewendet: Die Finite-Elemente-Methode (FEM) reduziert den datenmäßig erfassten Glockenkörper auf berechenbare Grundbausteine, d. h. sie teilt die Glockenwand in kleine Ringelemente ein und errechnet aus ihnen bei bekannten Materialeigenschaften die Frequenzen der Eigenschwingungen. 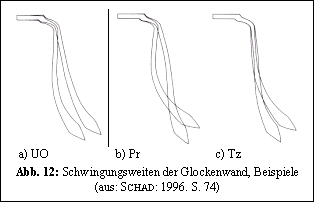Da FEM auch die Verformung der Struktur angibt, können in erzeugten Bildern die Schwingungsbäuche und -knoten an der Graufärbung der Glocke abgelesen werden. In Abbildung 11 sind Beispiele dieser Klangfiguren dargestellt. Im Querschnitt und linear vergrößert kann man in Abb. 12 die Schwingungsweiten der Glockenwand miteinander vergleichen. (Abkürzungen der Teiltöne siehe Tab. 1)


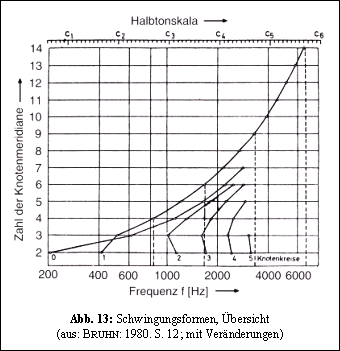
	Abbildung 13 zeigt am Beispiel einer as'-Glocke die Zuordnung von Knotenkreisen, Knotenmeridianen und Schwingungsfrequenzen. Zum richtigen Verständnis der Grafik muss man beachten, dass nur an den Punkten, an denen sich die Linien der Knotenkreise mit den Linien der Meridiane schneiden, eine Schwingungsform mit ihrer Eigenfrequenz ablesbar ist.

In der Tendenz zeigt sich, dass Schwingungsformen mit einer größeren Anzahl von Knotenkreisen bzw. Knotenmeridianen auch größere Eigenfrequenzen besitzen. Die senkrecht gestrichelten Linien heben die Oktavabstände oberhalb der Prime hervor. Auffällig ist, dass diese Oktavabstände immer eine Schwingungsform mit genau einem Knotenkreis (r = 1) treffen. (Darunter ist auch die Prime.) Die zugehörigen Teiltöne, nämlich Oberoktave, Doppeloktave, Tripeloktave usw., besitzen für den Glockenklang eine besondere Bedeutung. Sie zählen neben der Unteroktave (r = 0, m = 2) zu den sog. Lauttönern einer Glocke. "Lauttöner" sind die Teiltöne, die im Klangspektrum der Glocke am stärksten hervortreten, weil sie meist in der Nähe des Schlagrings ein Schwingungsmaximum besitzen und deshalb beim Klöppelanschlag stark erregt werden. Die Lauttöner ab der Oberoktave haben auch für den Schlagton eine Bedeutung, die im nächsten Abschnitt behandelt wird.

Hier soll natürlich keine vollständige Auflistung aller Teiltöne mit Namen und Schwingungsform erfolgen, dafür gibt es entsprechend ausführliche Literatur, sondern es sind nur einige Beispiele ausgewählt, die zeigen, wie die Glockenschwingungen aussehen und was charakteristisch für sie ist. Vergleicht man obige Abbildung 13 mit Tabelle 1, so erkennt man auch, dass es viel mehr mögliche Schwingungsformen als wirklich deutlich feststellbare Teiltöne im Klangspektrum einer Glocke gibt. Das liegt daran, dass diese Eigenfrequenzen längst nicht alle so stark angeregt werden, um als eigener Teilton berücksichtigt werden zu können.